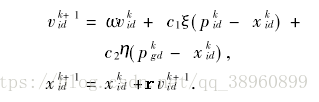————-正文
首先,我是参考的这个专栏的博文,感觉理解起来还行,但是由于我个人的原因,时间的关系暂时先做如下总结,往后有机会再拾起的研究的话再更新更正。如果有什么理解不对的或者需要补充的,欢迎各位指正,谢谢。
什么是粒子群算法?
总结起来说,就是有自主意识的粒子,什么样的意识?可以依据某种规则(意愿)去寻找某些东西。说得官方一些,就是寻找最优解的一种算法。至于为什么叫做粒子呢?我猜是因为他模拟了粒子的不确定性(数量,维度,速度足够多的不确定性)。就和其他介绍里说的,那是模仿鸟类觅食的过程,是相近的。
在以上的博文中提到了,我在这里引用一下:
CAS系统中的主体具有4个基本特点
- 首先,主体是主动的、活动的。
- 主体与环境及其他主体是相互影响、相互作用的,这种影响是系统发展变化的主要动力。
- 环境的影响是宏观的,主体之间的影响是微观的,宏观与微观要有机结合。
- 最后,整个系统可能还要受一些随机因素的影响。
ok,我们已经知道了他这个粒子群算法的目的是为了寻找某个事件或者某个过程的最优解。那么我以我上面参考的那个博文为例(因为我也只研究到了那一步而已),他是以一个函数为例,最优解就是寻找这个函数在某个定义域内的最大值点的坐标,也即找最大值。(寻找最大值貌似也挺简单的,可能只是例子的原因吧,mark)那么我们可以这么做,在定义域内,随机生成两个点,也就是代表有两个粒子(至于你想要多少个粒子,你可以自己根据自己的需求),而函数有多少个解就表示该粒子有多少维度,这个也很好理解吧,如果有两个地方放置食物,那么鸟类的属性中就会有两个地方的距离信息,也就是二维的,当然情况肯定是维度越高越复杂了。然后我们的主体有了——粒子,那么我们还需要他移动,怎么移动,往哪移,移多少这套规则是在一个位置速度更新公式里决定的。什么时候算是找到食物呢?这就是需要适应度函数来判定了。在这个例子里,就是判断函数值的大小,至于采取怎么样的判断方法,怎么样才更科学,更有效,那就是适应度函数的优略了。
以上对应于博文的就是:
- 这两个点就是粒子群算法中的粒子。
- 该函数的最大值就是鸟群中的食物
- 计算两个点函数值就是粒子群算法中的适应值,计算用的函数就是粒子群算法中的适应度函数。
- 更新自己位置的一定公式就是粒子群算法中的位置速度更新公式
好,我们就可以完成粒子属性的初始化了,如果是写c的话,一个结构体已经诞生了。一个粒子就是一个结构体,当然这还步完善。我们继续。
接下来就是研究粒子的运动机制了。在博文中,有一个位置速度更新公式:
大家也可以去博文上看看,我这里就厚脸皮的直接复制过来了。还有一下重要的参数介绍:
是保持原来速度的系数,所以叫做惯性权重。
是粒子跟踪自己历史最优值的权重系数,它表示粒子自身的认识,所以叫“认知”。通常设置为2。
是粒子跟踪群体最优值的权重系数,它表示粒子对整个群体知识的认识,所以叫做“社会知识”,经常叫做“社会”。通常设置为2。
是[0,1]区间内均匀分布的随机数。
是对位置更新的时候,在速度前面加的一个系数,这个系数我们叫做约束因子。通常设置为1。
也就是说,根据以上的公式,我们就可以速度和位置了。以上的参数应该就需要自己针对应用场景做出相应的调整了,或者有什么自适应的操作,我这里就不研究了。总之,我们是可以控制粒子的速度和位置的。通过观察,我们发现他是需要到新、旧速度,新、旧位置的,所以我们的结构体就需要增加两个粒子的属性了。
这样以后,我们就可以不断的进行迭代循环不断进行寻找“食物”了,这时,我们可以通过适应度函数达到和最优解相差不小的时候停止输出,或者循环多少次后结束这都可以,看你的需求了。
好了,整体的粒子群算法思路就是这样。还需解决的问题有,优化问题,实际应用的转换问题,也即我们在实际使用的时候,是怎么使用的呢?